Kth Problem (Selection Problem)

---

Begin with a problem

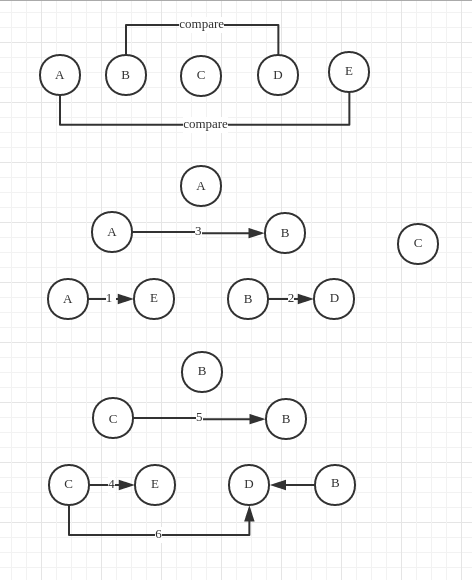
“compare six times to find the third small number of five numbers”

Analysis process:

1. First, come up with the solution of sorting

   • Using the sort by comparison cost $O(n\log_2n)$, like quicksort or mergesort;
   • then choose the one with constant time;
   • but it’s not good enough for this problem

2. The second thought: Try blindly – 7 times in the worst case

3. The third one: realize the differences between “find the k th small number” between sort:

   • when to find the k-th small number, we don’t need to know the order of other numbers, so if we sort them, we will do many useless work.

4. The forth one: realize the “find the k th small number” and sort are similar in essence

   • If we deem sorting as cancel the possibility like Knuth¹ said (choosing a permutation of the input), the k-th small number is also choose some permutations of the input.

Abstraction of problem

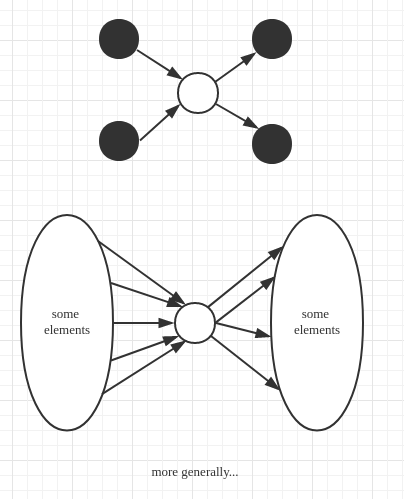
A demonstration

The following graph is the demonstration of above problem:

Description

• We just want the third number, so which one is the first or second may not be a must. Try to avoid useless order so as to save comparison.
• More generally, we only have to know the one larger than $(k-1)$ elements, smaller than $(n-k)$ elements. So the lower bound of this problem is $O(n)$

Perspective one – rule out more possibilities

Introduction

As we have mentioned, the problem can be seen as the process of ruling out possibilities of permutations.

suppose an array $a$ of length n $: a_1, a_2, ... , a_n$

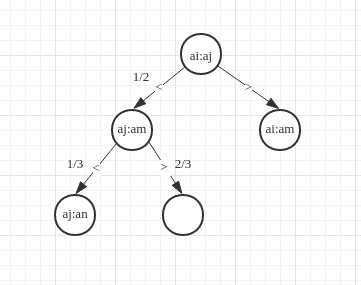
If we choose two numbers at random to compare and get the following result:

$a_i < a_j$ : (Any) comparison result can exclude half possibilities of all permutations of array a

Then, if we compare $a_i$ or ($a_j$) with the third element ($a_m$), the third element has three possible locations:

here $a_i$ here $a_j$ here

but compare with any of $a_i$ or $a_j$, we can exclude $1/3$ or $2/3$ possibilities, so on so forth. And this process is shown in decision tree model of comparison sort ².

We can conclude that by one comparison, excluding $1/2$ possibilities is the best case.

Application – make use of $1 \over 2$

1. Compare different elements
   Taking the problem we mentioned at the beginning of the article as an example.
   Basic:
   • Five numbers: $5!$ possibilities
   • the middle one is settled: $2! * 2!$ possibilities are accepted: so there is $30 = 5! / 4$ possibilities to exclude.

Since we have the principle, through some trial and error, we can come up with the following approach to solve the problem. (one tricky step is to ignore the smallest one of 4 number – ie, A and B, for it can’t be the median)

> the possibilities remaining after every comparison:  
> $1/2 * 1/2 * 3/5 * 1/2 * 3/5 * 2/3$

2. Method like quicksort – choose a good pivot
   Before we dive into this solution, let’s study why quick-sort is so fast and why a good pivot can be very important for quicksort.

Basic:

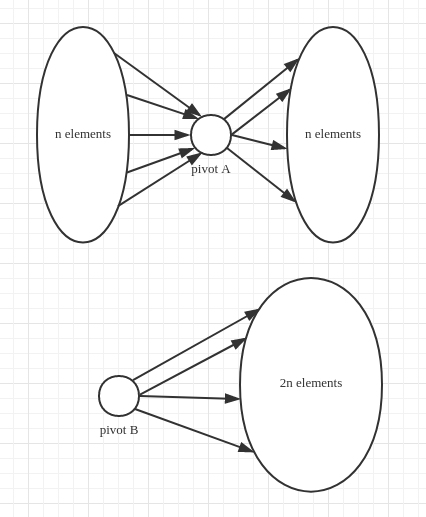
• the critical procedure of quicksort – partition: choose a pivot and compare other elements with pivot.
  In the following graph, the pivot A is very good for the elements is separated evenly around it, so if you compare it with one more element it will rule out $50\%$ possibilities. On the other hand, the pivot B is very bad and one more comparison can only rule out $1\over(2n+1)$ possibilities in worse case.

Analysis:
on average, the pivot is not as good as pivot A but also as bad as pivot B, so quick-sort can have a recursion tree whose height is proportional to $log_2n$. And the better the pivot is, the less the recursions happen, the faster the sort proceeds.

---

---

**To be continued **

Perspective two – Save some comparison results

Tournament Tree (Winner Tree)

Heap

More

Using a way like linear sort?

Reference

1. Order statistic
2. 数学之美番外篇：快排为什么那样快

Written with StackEdit.

---

1. Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Second Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Chapter Five - Sorting ↩︎

2. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). “8 Sorting in Linear Time”. Introduction to Algorithms (3rd ed.). MIT Press & McGraw-Hill. ISBN 0-262-03293-7. ↩︎